|

HOME >수학이야기>송영준의 수학따지기
|
|
|
|
|
Posted at 2012-01-19 13:11:35
|
이 글은 사단법인
전국수학교사모임의 회지인 '수학과교육' 2007년
7/8월호에 실렸던 필자의
글을 편집한 것입니다.
따짐이
: 선생님, 수학의
'수'는 우리가 흔히
말하는 그 '수' 지요?
선생님
: 그렇지. 설마 물이라는
뜻이겠니?
따짐이
: 헐
~ '물' 끼얹은 듯
썰렁하네요. 어쨌든, 그럼 수학이 수에
대한 학문이라는 뜻인 것 맞네요?
선생님
: 말뜻은
그렇지. 하지만 수학이 수만
다루는 것은 아니라는 것은 너도 알지?
따짐이
: 원래는
그랬지요?
선생님
: 그것도
아니야. 수학이라는 표현은
우리나라, 일본, 중국 등에서
쓰이고, 영어의
mathematics
처럼 유럽 언어에서는 수와는 직접 관련이 없는 말이 쓰이니까, 고대로부터 수학이라는
말은
수와 도형의 연구를 함께 가리켰다고 할 수 있지. 학교에서 배우는
교과서 내용도 크게 수와
도형에
대한 것으로 나눌 수 있지 않니?
따짐이
: 제가 하려는 말이 그
말이거든요. 수와 도형으로 잘
나가다가...
선생님 : 나가다가? 따짐이 : 문자. 그리고 ‘식’ 이라는 것이 나오는데 그것들의 정체를 잘 모르겠어요. 선생님 : 왜 그렇지? 따짐이 : 수끼리 계산하면 하나의 수가 답으로 나오잖아요? 그런데 식끼리 덧셈, 뺄셈, 곱셈 같은 계산 을하면 답이 식이더군요.
선생님 : 그게 어때서? 따짐이 : 예를 들면, 2x+3y에서 x-6을 빼면 답이 x+3y+6이 되잖아요? 선생님 : 그렇지. 따짐이 : 그리고 (2x+3y)-(x-6)도 식이고 x+3y+6도 식이죠? 선생님 : 그래. 따짐이 : 어차피 앞의 것도 식이고 뒤의 것도 식인데, 앞의 것을 뒤의 것으로 고치고서는 그걸 ‘계산’ 했다고 할 수 있나요? 선생님 : 식의 계산은 원래 그런 거니까. 따짐이 : 2+5를 계산해서 7이라고 할 때는, 그 사이에 분명히 다른 점이 있지요. 2+5는 하나의 수가 아닌데 7은 하나의 수이니까. 선생님 : 글쎄... 그럼 이건 어때? 따짐이 : 뭐요? 선생님 :  따짐이 : 그래서요? 선생님 : 답이라고 하는 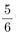 말인데, 그게 하나의 수인가? 5를 6으로 나누라는 뜻 아닌가? 말인데, 그게 하나의 수인가? 5를 6으로 나누라는 뜻 아닌가? 따짐이 : 응? 그러고 보니 그런 것 같기도... 선생님 : 사실은 그렇지 않아. 따짐이 : 그, 그렇죠.  는 하나의 유리수인데, 그것을 그렇게 표현하는 것뿐이니까. 수직선에 찍어보면 는 하나의 유리수인데, 그것을 그렇게 표현하는 것뿐이니까. 수직선에 찍어보면  는 하나의 점에 불과하잖아요? 는 하나의 점에 불과하잖아요? 선생님 : 그럼 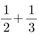 은? 그건 수직선에 찍으면 한 점이 아닌가? 은? 그건 수직선에 찍으면 한 점이 아닌가? 따짐이 : 음...아무래도 제가 단순했나 보네요. 선생님 : 그래.  에서, 좌변이건 우변이건 사실은 하나의 수를 말하는데 표현 방법이 다른 뿐이지. 에서, 좌변이건 우변이건 사실은 하나의 수를 말하는데 표현 방법이 다른 뿐이지. 따짐이 : 그럼 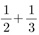 의 ‘표현 방법을 고쳐서’ 의 ‘표현 방법을 고쳐서’ 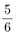 로 만드는 것을 가리켜 덧셈을 한다고 하는 이유는 로 만드는 것을 가리켜 덧셈을 한다고 하는 이유는 무엇인가요? 선생님 : 덧셈이 원래 그런 거니까. a+b의 형태를 갖는 것을 c의 형태를 갖도록 고치는 것을 가리켜, a와 b를 더하여 c를 계산했다고 하는거지. 따짐이 : 뭔가 내용이 없는 듯한 느낌이.... 선생님 : 하지만 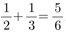 과 같은 등식은 분명히 내용을 담고 있어. 과 같은 등식은 분명히 내용을 담고 있어. 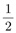 로 표현되는 유리수와 로 표현되는 유리수와  로 표현되는 유리수를 더하여 만든 로 표현되는 유리수를 더하여 만든  이라는 새로운 유리수는 이라는 새로운 유리수는  으로도 표현된다는 내용을. 으로도 표현된다는 내용을. 따짐이 : 좋아요. 그건 그렇다 치고, (2x+3y)-(x-6)을 계산하여 x+3y+6을 만드는 것은... 이것도 같은 식인데 표현을 달리 한 것이라는 거죠? 선생님 : 그렇지. 네 말대로 양쪽 모두 식이고, 표현을 달리한 것뿐이지만 그래도 의미는 있지. 원래 있던 괄호 도 없어지고, 동류항도 하나로 정리되었고, 어쨌든 더 간단해졌으니까. 그래서 교과서를 보면 식의 계산 문제는 ‘단단히 하여라’로 끝나지 않니? 따짐이 : 더 간단히 만드는 것이 식의 계산의 목적이라는 건데...왜 간단히 하는 것이 중요할까요? 선생님 : 교과서를 보면 알 수 있을 걸? 식의 계산 다음에 나오는 것들을 보면... 따짐이 : 그게 뭔지 잘 모르겠는데요? 식의 산이 그 다음에 나오는 것들을 위한 중간 과정이라는 생각도 지금 까지는 안 들었는데...
선생님
: 그럼 지금이라도
생각을 해 보면 되지. 식을 간단히 하지
않고 계속 놔두면. 그것을 다른 목적에
사용
할 때, 예를 들어 또 다른
식과 계산을 한다든지, 두 식이 같은지
비교한다든지, 문자에 값을
대입한
다든지, 그 식과 관련된
방정식을 푼다든지 할 때 어떻게 될 것 같니?
따짐이
: 음... 식을 계산하면 할수록
점점 복잡해지겠지요? 지금 우리가 쓰는
이항이니 뭐니 하는 방법으로 방
정식을
풀기도 어렵겠고,,, 두 식이 같은지
비교하는 것은,,,,사실상
불가능하겠네요.
선생님
: 그래. 식을 가지고 우리가
하는 수많은 일들은 사실 식을 간단히 하는 기술이 있어야 가능한 것이지.
방정식, 부등식, 함수 같은 단원에서는
말할 것도 없고, 도형에서 길이나 넓이
같은 것을 다룰 때도
문자를 사용하고 식을 계산해야 하니까.
따짐이
: 계산이란 표현 방법을
바꾸는 것에 불과하다... 더 편리하고 유용하게
쓰기 위해서... 이건가요?
선생님
: 그래. 계산 자체가 목적이
될 수는 없지. 목적이 달라 다른
종류의 계산을 하는 경우도 있다는 것을
보면
그것을 알 수 있어. 자연수의
소인수분해나, 다항식의
인수분해, 그리고 하나의
분수였던 것을
몇 개의 분수의 합으로 고치는 ‘부분분수로
분해하기’ 같은 것들
말이야.
따짐이
: 맞아요. 그것들은, 왜 더 복잡한 쪽으로
바꾸는 계산을 하는 건지 이해가 잘 안 되었는데 이제 좀 알
겠네요. 약수를
구한다든지, 방정식을
푼다든지, 적분을 한다든지 하는
각각의 목적에는 간단한 형태
보다 그런 복잡한 형태가 더 편리하고 유용하기 때문이라는 거죠? 계산이란 목적에 맞게
표현방법을
바꾸는 거니까요.
|
|
|
|
|
|
|
|
|