문1>C는 선분 AB위의 한 점이고 그림과 같이 AB에 대하여 같은 쪽에 두 점 D, E가 있고 삼각형 ACD, BCE가 정삼각형이면
AE와 CD의 교점이 P, BD와 CE의 교점이 Q일 때 CP=CQ임을 보여라.
문2> 그림과 같이 삼각형 내부의 한 점 P를 지나며 세 변에 평행인 세 직선은 삼각형을 여섯 부분으로 나눈다. 그 중 세 개의
삼각형의 넓이를 각각 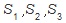 [0]#wh4/4.3`5.6/11,[1]{{S}_{1}}[0]#wh4/4.3`5.6/11,[1]{{S}_{2}}[0]#wh4/4.3`5.6/11,[1]{{S}_{3}}라고
할 때 원래의 삼각형의 넓이를  [0]#wh4/4.3`5.6/11,[1]{{S}_{1}}[0]#wh4/4.3`5.6/11,[1]{{S}_{2}}[0]#wh4/4.3`5.6/11,[1]{{S}_{3}}으로
나타내시오.
이 두 문제좀 풀어주세요.. 푸는 법이 잘 생각나지 않네요.. |
