이현녀 선생님의 답변입니다.
1. 정석책(실력수2 or 실력미적)에서 보면
함수 f(x)가 어떤구간에서 미분가능하고 그
구간에서
항상 f'(x) > o 이면 f(x)는 그 구간에서 증가하고
항상
f'(x) < o 이면 f(x)는 그 구간에서 감소한다.
라고 되어있는데 만약
어떤구간이 폐구간이라면
그 폐구간의 끝값에서는 미분이 불가능하니 저 말자체로는 모순아닌가요?
구간에서의 증가, 감소는 점에서의 증가, 감소 상태가 무엇을 말하는지 먼저 알아야 합니다.
점에서의 증가, 감소 상태라함은 한 점과 그 점에 충분히 가까운 앞 뒤 근방의 점들과 비교하여
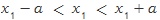 일 때,
일 때, 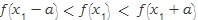 이면 함수
이면 함수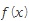 는
는 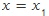 에서 증가상태에 있다고 말한다. 즉, x
값이 커질수록 함수값 y 도 커지는 상태를 말한다.
에서 증가상태에 있다고 말한다. 즉, x
값이 커질수록 함수값 y 도 커지는 상태를 말한다.
따라서 함수의 끝점에서는 한쪽 근방은 있으나 다른 쪽 근방이 없기 때문에 일반적으로 증가, 감소 상태를 말하지 않습니다.
2. 어떤구간에서의 특정 한점에서만 미분 불가능이고 나머지 부분에선 미분가능할때
그 나머지 모든
구간에서 f'(x) > o(or f'(x)< o) 이면 이 함수는 증가(or 감소)라고 할수 있나요? (실력정석 미적 132p 유제
8-3)
보통은 그렇다고 생각합니다. 아직은 그렇지 않은 경우는 못 본 듯 합니다.
3. 실력미적에서 함수의 증가를 평균값의 정리로 증명했던데..
i) 만약에 어떤구간이 폐구간이면
f'(c)자체를 정의할수 없지않습니까?
왜냐하면 c는 어떤구간의 임의의 두값 x1,x2의 사이에 존재하기 때문입니다.
따라서 구간이
폐구간이면 c는 그 끝값에선 정의가 안되는 것이죠..
ii) f(x2)-f(x1)=f'(c)(x2-x1)에서 f'(c)=o 이면
f(x1)=f(x2) 이므로 증가가 아니게
되는데요. 그런데 f'(x)=o 이어도 증가상태인 경우는 있는데 이것은 어떻게
설명해야
합니까.
1번을 이해하면 이것도 이해가능하리라 생각됩니다. f'(c)=o 일 때는 c 를 기준으로 양쪽의 상태가 서로 반대이죠. 한 쪽은 증가, 다른 쪽은 감소 상태랍니다.
4. 증가의 정의가 'x1<x2 이면 f(x1)<f(x2)이다'인데, 이 명제의 역은
성립하지않는
것도 아닌데 왜 한쪽방향으로만 화살표가 가는겁니까? 특별한 이유가 있나요
보통 x 를 독립변수, y 를 종속변수로 생각하기 때문에 x 값에 따른 y 의 변화를 말하는 겁니다. y 를 먼저 말하고 x 를
나중에 말한다고 달라지지는 않습니다.
5. 어떤 폐구간 끝점에서의 증가감소를 정의할때 기타 개념설명부탁드립니다.
(ex. 그점에서의
미분계수는 증가감소와 상관없다든지...아니면, 이러이러한 조건을 만족해야 성립한다든지 등등..)
이것도 1번 문제에서 이해가능하였으리라 생각합니다.
이로소 정확한 이해가 얼마나 중요한 지 아셨지요? 그래서 수학 교과서를 읽고 읽고 또 읽어 내용을 충분히 숙지하는 것이 문제를
많이 푸는 것보다도 더더욱 중요한 것입니다.