|
|
|
|
|
Posted at 2012-01-27 13:10:54
|
이현녀 선생님의 답변입니다.
모두 답은 알고 있는데 풀이를 잘모르겠어요 풀이 설명좀 부탁드립니다.
1. 12명의 유권자가 3명의 후보자 중에서 한 사람을 선출할 때 몇가지 투표결과가 생기는가 단
기명투표이며 기권과 무효는 허용하지 않는다.
답:531
답변해주시면 감사하겠습니다. 그런데 이 수식 프로그램 익스플로어 오류가 너무 잘나는것 같아요, 벌써
세번째 시도인데;; 너무 힘듭니다 ;;
먼저 오류가 많은 점 인정하고 죄송합니다. 우리나라에서 최초로 게시판에 수식과 도형이 함께 가능한 게시판이라 그런 것 같습니다. 또 더
많은 사람들이 연구하면 아마도 더 나아지리라 기대합니다.
1. 답이 틀린 것 같네요. 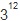 =531441 인 것 같습니다. =531441 인 것 같습니다.
모든 사람이 한 명씩 선출이 가능하기 때문에 12명이 모두 A를 뽑을 수도 있고, 12명이 모두 B를, 또는 모두 C를 선출할 수도 있기
때문에 A, B, C 세 명 중 중복을 허락하여 12번 뽑는 경우의 수를 말합니다. (1번이 선출가능한 경우의 수 3, 2번도 선출가능한 경우의
수가 3 , ... 해서)
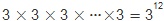 입니다. 입니다.
2. 5개의 숫자 0,1,2,3,4 중에서 서로 다른 3개의 숫자를 택하여 만든 세자리 정수의 총합은 ?
답:12990
5개의 숫자 0, 1, 2, 3, 4 중에서 서로 다른 3개의 숫자를 택하여 만든 세자리 정수의 개수는 모두 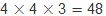 개입니다. 개입니다.
이 중 백의 자리에 올 수 있는 수는 1,2,3,4 넷이므로 각각  = 12번씩 들어갑니다. 따라서
백의 자리의 수의 합은 (100+200+300+400)×12=12000 = 12번씩 들어갑니다. 따라서
백의 자리의 수의 합은 (100+200+300+400)×12=12000
십의 자리에 올 수 있는 수는 백의 자리에 온 수를 제외한 0을 포함한 4개의 수이므로 0을 뺀 부분의 비율은 전체의 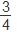 이다. 이다.
따라서  이고 네 수로 나누면
9번씩 들어갑니다. 이고 네 수로 나누면
9번씩 들어갑니다.
십의 자리의 수의 합은 (10+20+30+40) × 9=900
일의 자리에 올 수 있는 수는 십의 자리에 올 수 있는 수와 마찬가지 방법으로 하면
일의 자리의 수의 합은 (1+2+3+4) × 9=90
따라서 총 합은 12990 입니다.
3. 품질이 같은 사과 7개와 배 6개를 4명의 아이에게 모드 나눠주는 경우의 수는? 단. 모든
아이에게 적어도 사과와 배를 한 개씩 주어야 한다.
답: 200
이 문제는 적어도 사과와 배를 한 개씩 주는 행동을 먼저 하면, 남은 사과 3개, 배 2개를 4명에게 나누어주는 경우의 수를 구하는
문제입니다.
사과 3개를 4명에게 나누어 주는 가지수는 A, B, C, D 네 명 중 중복을 허락하여 3명을 선택하면 되므로 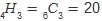 , ,
마찬가지로 배 2개를 4명에게 나누어 주는 가지수는 A, B, C, D 네 명 중 중복을 허락하여 2명을 선택하면 되므로  이다. 이다.
따라서 사과를 나누어 주는 경우와 배를 나누어주는 경우는 서로 독립이므로 구하는 전체 경우의 수는
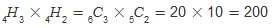 입니다. 입니다.
4. A=(1,2,3,4,5) B=(1,2,3)
B에서 A로의 함수 f 가 f(1)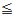 f(2) f(2) f(3) 이 되는 경우의 수는
? f(3) 이 되는 경우의 수는
?
답 : 35
B={1, 2, 3} 에서 A={1, 2, 3, 4, 5} 로의 함수
f 가 f(1) f(2) f(2) f(3) 이 되는 경우의
수는, f(3) 이 되는 경우의
수는,
함수값만 세 개 순서쌍으로 쓰면 (1, 1, 1), (1, 1, 2), (1, 1, 3),
과 같이 열거될 수 있으므로 1, 2, 3, 4, 5 다섯 개의 숫자 중 중복을 허락하여 3개를 뽑는 경우의 수와
같다.
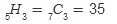
|
|
|
|
|
|