윤상호 선생님의 답변입니다.
우선 1번은 참이고, 2번은 거짓입니다. 따라서 1번은 증명을 2번은 반례를 들겠습니다.
[1번 증명]
lim An = 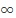 라는 이야기는 임의의
큰 양수 M>0에 대해서 n이 충분히 크면 모든 An > M이란 얘기입니다. 라는 이야기는 임의의
큰 양수 M>0에 대해서 n이 충분히 크면 모든 An > M이란 얘기입니다.
Bn > An 이므로, 충분히 큰 n에 대해서 Bn > An > M 입니다.
즉, lim Bn =  입니다. 입니다.
[2번 반례]
1 < 1+ 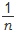 이지만, lim 1 = 1 =
lim (1+ 이지만, lim 1 = 1 =
lim (1+  ) 입니다. ) 입니다.
이 명제를 참으로 만들려면, 극한에 있는 부등호에 =을 추가시켜주면 됩니다. |