다음글	질문
이전글	기하문제를 잘 풀고 싶습니다 ㅜㅜ
답글	세원이 접할 때 생기는 원의 반지름 답변

<P>이현녀&nbsp;선생님의 답변입니다.</P> <P>&nbsp;</P> <P>&nbsp;</P> <DIV class=board> <P><FONT color=#0000ff>반지름이 각각 1cm, 2cm, 3cm인 세 원이 서로 각각 접하고 있을 때</FONT></P> <P><FONT color=#0000ff>접하고 있는 가운데 빈 공간 부분에 만들어질 수 있는 원의 반지름을 어떻게 구하는지요?</FONT></P> <P>&nbsp;</P> <P>&nbsp;</P> <P align=center></P> <P align=left><img onLoad='miniSelfResize(contents_1996,this); if(this.parentNode.tagName=="A"){this.onclick = "";}' src="/shop/lib/meditor/../../data/editor/1326962221.jpg"></P> <P align=left>&nbsp;</P> <P align=left>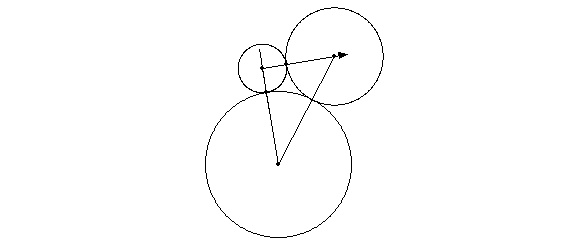그림에서 알 수 있듯이 반지름의 길이가 1,2,3인 원이 접할 때 중심을 연결하면 변의 비는 3:4:5이므로 직각삼각형이 됩니다. </P> <P align=left>따라서 직각인 두 변을 좌표축으로 하여 좌표평면에 세 원을 그리면 반지름이 1인 원은 중심이 원점이고, 반지름이 2인 원과 반지름이 3인 원은 중심이 각각 x축, y축 위에 놓이게 됩니다. 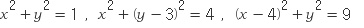즉</P> <P align=left><img onLoad='miniSelfResize(contents_1996,this); if(this.parentNode.tagName=="A"){this.onclick = "";}' src="/shop/lib/meditor/../../data/editor/1326962247.jpg"></P> <P align=left></P> <P align=left>그리고 세 원에 접하는 원의 방정식은 중심을 (a, b) 반지름을 r 이라 놓으면&nbsp;</P> <P align=left><img onLoad='miniSelfResize(contents_1996,this); if(this.parentNode.tagName=="A"){this.onclick = "";}' src="/shop/lib/meditor/../../data/editor/1326962261.jpg"></P> <P align=left></P> <P align=left>중심과 중심 사이의 거리를 이용하면 세 방정식이 나옵니다.</P> <P align=left><img onLoad='miniSelfResize(contents_1996,this); if(this.parentNode.tagName=="A"){this.onclick = "";}' src="/shop/lib/meditor/../../data/editor/1326962288.jpg"></P> <P align=left></P> <P align=left>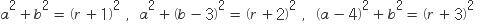위 세 식을 연립하여 풀면 </P> <P align=left><img onLoad='miniSelfResize(contents_1996,this); if(this.parentNode.tagName=="A"){this.onclick = "";}' src="/shop/lib/meditor/../../data/editor/1326962313.jpg"></P> <P align=left></P> <P align=left>이 나오네요.</P></DIV>