이현녀 선생님의 답변입니다.
문제의 초점은
(1) 명제 "두 개의 닮음도형에서 대응하는 점들을 이은 직선이 모두 한 점에서 만나고 그 점에서
대응하는 점들까지의 거리의 비가 일정하다" 가 참인가 하는 것입니다
이 문제는 전제조건이 두 개의 닮음도형입니다.
따라서 닮은 두 도형은 이미 대응하는 점들이 있습니다.
예를 들어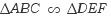 
이라고 할 때,
점 A의 대응점은 D이고, 점 B의 대응점은 E, 점 C의 대응점은 F 입니다.
이 두 도형이 닮음도형이더라도 두 삼각형이 닮음의 위치에 있지 않으면 대응점끼리 연결하더라도 한 점에서 만나지 않습니다. 때문에 거리의
비가 일정하지도 않지요.
쉽게 생각하여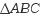 
를 두 배로
확대하여 
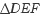를 만든 뒤 약간 비틀어
놓으면(회전이동) 두 닮음 도형은 닮음의 위치에 있다고 말 할 수 없습니다.
따라서 위 문장은 거짓이고, 참이 되게 바꾼다면 다음과 같겠지요.
"두 개의 닮음도형에서 대응하는 점들을 이은 직선이 모두 한 점에서 만난다면 그 점(닮음의
중심)에서 대응하는 점들까지의 거리의 비는 항상 일정하다"
(2) 위의 명제에서 대응하는 이라는 용어의 해석부분입니다. 이현녀 님께서는 이 부분을 끝점은 끝점끼리
중점은 중점끼리 1/4점은 1/4점끼리 대응하여야 한다고 해석하신듯 합니다만 위의 명제에서 반드시 그렇게 해야 된다는 전제가 없을
뿐더러 선분으로 이루어진 도형(다각형)외에 예를 들어 포물선이나 그 밖의 일반적인 곡선으로 이루어진 도형에는 어떻게 적용해야 하는지
의문이 갑니다.
'대응'은 수학적 용어입니다. 두 개의 닮은도형이나 합동인 도형에서 서로 같은 또는 짝이 되는 위치의 각 또는 점에 대응이라는 용어를
사용합니다.
예를 들어 30-60-90도인 두 닮음삼각형에서 대응하는 각은 같은 각을 말하고 대응하는 변은 같은 각을 사이의 변들끼리를
말합니다.
따라서 확장하면 선분은 점이 모여 이루어지므로 중점의 대응점은 중점이어야하겠지요.
다각형이 아닌 포물선과 같은 도형은 그 특징을 생각하면 간단합니다.
포물선에는 꼭지점이 있고 항상 꼭지점을 기준으로 포물선의 축에서 떨어져 있는 거리가 같은 것끼리 대응점이 되겠지요.
타원도 두 초점을 중심으로 , 또는 장축과 단축을 기준으로
쌍곡선도 두 초점 또는 점근선을 기준으로,
물론 원은 어떻게 말해도 상관은 없겠지만 원의 중심을 기준으로 대응점을 찾을 수 있으리라 봅니다. 그 밖의 일반적인 도형들도 닮은도형이라면
대응점을 찾는게 어렵지는 않을 것입니다.
좋은 답변 부탁드립니다.
이현녀님 새해에도 항상 행복하시고 건강하세요^0^
p.s 저는 선생님의 팬입니다^^^
선생님께서 이렇게 좋게 봐주시니 감사합니다.
더 많은 이야기를 하고 싶네요. 연락주시면 더 좋겠습니다. san11@mathlove.com 이현녀입니다.
