이현녀 선생님의 답변입니다.
조선시대 홍길주의 제곱근 풀이법이 어떤 방법인지 궁금합니다.
언론 기사에 나온 내용만으로는
그 풀이법을 자세히 알기가 어려운 것 같습니다.
123.456 이라는 값의 제곱근, 세제곱근, 네제곱근... 등을
'홍길주 풀이법'으로 구하는 방법을 알려주세요...
신문의 기사에 의하면 서울대 연구원이 논문에 발표한 내용 중 일부만이 나와있네요.
물론 논문을 뒤져보면 알 수도 있겠으나 그 방법이 비록 우리 선조가 발견한 것이기는 하지만 그리 우수하다고는 볼 수 없다는 여러 선생님들의
의견과 더불어 제가 해 보니 제곱수가 아닌 경우는 이 방법으로 제곱근을 구할 수 없다는 결론이 나왔습니다.
신문 내용은 이렇습니다. 어떤수의 제곱이 x 라면, 그 수의 반을 구한다. 거기서 자연수 1 부터 차례로 뺀다. 음수가 나오지 않는
범위에서 자연수를 차례로 최대한 뺐을때 마지막 남은 수의 두 배가 다음 뺄 수와 같으면 다음 뺄 수가 바로 원래 수의 제곱근이다.
수열의 합을 이용한 증명은 다음과 같습니다.
수열의 합 공식 중 자연수의 합을 구하는 공식은
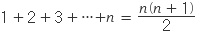
입니다. (참고 : 가우스가 9살 때 발견한 방법)
위 식을 다시 재 배열하면
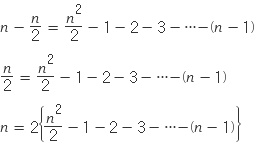
그런데 이 단 점은 제곱근이 자연수일 때만 성립합니다. 왜냐하면 자연수의 합 공식을 이용했기 때문입니다.
단적으로 제곱하여 2 가 되는 수를 위와 같이 찾으면
2의 반은 1 이고 여기서 첫번째 자연수 1을 빼면 0입니다. 물론 0의 두 배는 2가 아니지요.
따라서 모든 수의 제곱근을 위와 같이 구할 수 있는 것이 아니라 제곱수의 제곱근만 위와 같이 구할 수 있다는 것입니다. 또한 음수는
안되지요.
마찬가지 방법으로 세제곱근과 네제곱근도 자연수의 세제곱과 네제곱인 수들만 해당사항이 있기 때문에 굳이 이렇게 찾을 의미가 없을 듯
합니다.
그렇지만 님의 덕분에 또 하나의 생각을 해 보게 되어 참으로 행복했습니다^^ 감사합니다~~~~
|