이현녀 선생님의 답변입니다.
안녕하세요.
수2 함수의 극한 많이 어려워서 질문합니다.. ^^;;
1. 0/0 꼴 에선 "분모 g(x)가 x -> a에서 0이 된다고 하면 g(x)는 (x-a)를
인수로 갖고 이 때 극한값을 가지기 위해서 분자f(x)도 (x-a)를 인수로 가져
분모g(x)의 인수를 제거해야 한다"
극한값이란 하나의 숫자로 수렴한다는 겁니다. 따라서 극한값은 하나의 수로 나와야합니다. 수는 분모가 0 이
될 수 없습니다.
인수정리에 의하여 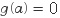 이면 이면 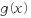 는 는 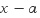 를 인수로 갖습니다. 를 인수로 갖습니다.
그런데 분모가 0 이라면 그것은 수를 벗어나기 때문에, 따라서 분자도 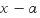 를 인수로 갖어야만 분모의 를 인수로 갖어야만 분모의
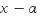 가 약분되어 없어지고
따라서 분모가 0 이 아닌 수로 나오는 것이 가능합니다. 가 약분되어 없어지고
따라서 분모가 0 이 아닌 수로 나오는 것이 가능합니다.
만약 극한값이 존재한다는 말이 없다면 분자도 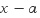 를 꼭 인수로 갖어야 하는 것은
아니겠지요. 를 꼭 인수로 갖어야 하는 것은
아니겠지요.
2. "극한값이 상수일 때 분모 0 -> 분자 0"
"극한값이 0아닌 상수 일 때 분자 0 -> 분모 0"으로 나눠져 있던데
"극한값이 0일 때 분자 0 -> 분모 0 "은 왜 성립이 안 되나요?
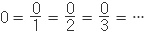 이므로 굳이
분모가 0 일 필요는 없지요. 이므로 굳이
분모가 0 일 필요는 없지요.
3. f(x)가 다항함수일 때만 미정계수가 결정되는 건가요?
제 생각엔 극한값에서의 미정계수를 말한다면 분자인 f(x)가 다항함수가 아닌 지수함수나 삼각함수, 로그함수인 경우는 별로 문제가
되지 않기 때문에 만들지 않는게 아닌가 싶네요. 문제를 만들려면 만들수도 있겠으나 만들어보니 너무 쉬워 말입니다. |