이현녀선생님의 답변입니다.
시그마의 합이 우변과 같이 "n의 제곱"의 형태로 나오는 것으로 보아 좌변이 등차수열의
일반항이라는 뜻인지요.
그렇다면, 등차수열의 일반항은 일차식의 형태라고 배웠는데 왜
앞과 같이 표현이 되는지, 또, 수열의 합이 n의 제곱의 형태로 나오는 수열이 등차수열 말고도 다른
수열이 존재하는지 궁금합니다.
님의 깊은 사고에, 함께 있는 선생님들이 너무너무 좋은 질문이라고 입에 침이 마르도록(^^) 칭찬을 아끼지
않으시네요.
수열의 합이 이차식인 경우는 일반항이 등차수열인 것은 맞습니다.
그래서 풀어보며 참 신기하다고 생각했습니다.
일반적으로 합의 기호(시그마)를 사용할 때는
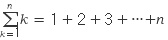
와 같이 한 문자 k에 관한 식으로 나타내고 그 값은 k 대신에 1부터 자연수를 차례대로 n까지 대입한 합이고 k 는 일반항을
의미하는 것이 보통인데
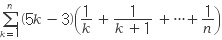
위 식은 한 문자 k 에 관한 식이 아니라 k 와 n 에 관한 식으로 되어
두 문자에 관한 식으로 되어있습니다. 따라서 합의 기호 옆에 붙어있는 식은 일반항의 의미가 되기 힘든 것입니다.
약식으로 다음 문제를 보십시오.
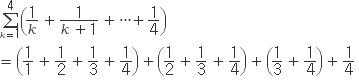
을 의미하므로 각각의 괄호 안을 하나의 항으로 본다면 등차수열이 될 수 없으나 분모가 같은 것들을 모으면 (1+1+1+1) 이 되어 공차가
0인 등차수열이 됩니다.
마찬가지로 위에 주어진 수능문제는 k 대신 1부터 n까지 차례대로 대입하면

아마도 이것은 배열을 달리하였을 때 등차수열의 합처럼 보이지 않는 모양이지만, 사실은 등차수열의 합인 것을 보이는 문제인 듯
합니다.
1부터 연속한 홀수의 합(1+3+5+7+9)이 한 수의 제곱이 되지만
1부터 연속한 자연수의 대칭수(1+2+3+4+5+4+3+2+1)의 합도 제곱수인 것처럼 정사각형을 어떤 배열로 보느냐에
따라 얼마든지 다양한 합으로 만들 수 있음과 같이 등차수열의 합도 다양한 모양으로 새롭게 만들 수 있음을 보여주는 예가 아닐까
합니다.
덕분에 저도 공부 많이 했습니다. 감사합니다. |